BLOQUE 5
UTILIZAS FUNCIONES FACTORIZABLES EN LA
RESOLUCION DE PROBLEMAS
Llamamos ceros o raíces de una función f a los valores de x para los cuales se cumple que f(x)=0. Los ceros de una función son las abscisas de los puntos en los cuales su gráfica tiene contacto con el eje de las x.
ACTIVIDAD 6:
Indicá los ceros de cada una de las funciones de la Actividad 5.
Recordá: Para hallar los ceros de una función de manera analítica, basta con igualar la ecuación a cero.
Ejemplo:
f(x)=x-2 Cero de f: x=2
x-2=0
x=0+2
x=2
Ejercicio 1:
función polinómica:
f(x) = 2x3 + 7x2 - 7x - 12
Y nos piden hallar los ceros. Los ceros o raíces de una función son las "x" para las cuales la "y" (ó f(x)) vale cero. Es decir: son los números a los cuales, si le aplicas la función, el resultado dá cero. Se pueden hallar "igualando a cero" la fórmula de la función, que es lo mismo que "reemplazar por cero" a la "y" o a f(x) de la fórmula:
2x3 + 7x2 - 7x - 12 = 0
f(x) = 2x3 + 7x2 - 7x - 12
Y nos piden hallar los ceros. Los ceros o raíces de una función son las "x" para las cuales la "y" (ó f(x)) vale cero. Es decir: son los números a los cuales, si le aplicas la función, el resultado dá cero. Se pueden hallar "igualando a cero" la fórmula de la función, que es lo mismo que "reemplazar por cero" a la "y" o a f(x) de la fórmula:
2x3 + 7x2 - 7x - 12 = 0
Ejercicio 2:
f(x) = x2 +
x - 12
|
x2 +
x - 12 = 0
|
Igualando
a cero.
|
(x +
4)(x - 3) = 0
|
Factorizando.
|
x = - 4
|
Solución
1
|
x = 3
|
Solución
2
|
Teoremas
del factor y del residuo
·
Algoritmo
de la división. Para cada polinomio
de grado mayor o igual a uno y para cada número
, existe un polinomio único
de un grado menor que el de
y un número único R, tal que:
Al polinomio
·
Teorema del
residuo. Si
es el residuo de dividir el polinomio
entre
, entonces
.
Demostración.
Como
O sea,
Ejemplo 1:
Hállese el residuo de dividir el polinomio
O sea que el residuo es 2.
·
Teorema del
factor. Si
es un cero del polinomio
, entonces
es un factor de
.
Demostración.
Si
Pero por el algoritmo de la división
Como
Por tanto,
Ejemplo 2:
Use el teorema del factor para probar que
Luego –1 es un cero de
Así
Division
sintetica
La división sintética es un
procedimiento "abreviado" para determinar el cociente y el residuo
que se obtiene al dividir un polinomio
de grado
, por un polinomio de la forma
, con
, a partir de los coeficiente de
y el cero de
.
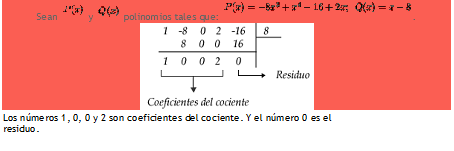
Ejemplo 1 :Sean
Teoremas
del factor y del residuo
El Teorema Fundamental del
Algebra (TFA) dice que todo polinomio a coeficientes complejos tiene un raíz
compleja, es decir existe un número complejo donde el polinomio evalúa a cero.
Hay muchas demostraciones de este importante resultado. Todas requieren
bastantes conocimientos matemáticos para formalizarlas, por ejemplo la división
sintética, el teorema del factor incluso el teorema del residuo. Sin embargo,
si se deja de lado algo del rigor matemático, hay argumentos simples y creíbles,
que le permiten a uno convencerse de la veracidad del TFA.
Este teorema resulta de suma
importancia dentro del estudio de las ecuaciones. Encontrar la solución de una
ecuación representa encontrar todos los valores de x para los cuales la
ecuación es cierta, a las que comúnmente le llamamos raíces de la ecuación,
generalmente las soluciones que de manera inmediata nos interesan son los
valores que existan en los reales, sin que con ello las soluciones complejas no
sean interesantes.
Teorema de factorización lineal
Si f(x) es
un polinomio de grado n, con n > 0, entonces f(x) tiene precisamente n
factores lineales, es decir:
f(x) = a(x – c1)(x – c2)....(x – cn),
factores lineales, es decir:
f(x) = a(x – c1)(x – c2)....(x – cn),
en donde
c1, c2, .....cn son números complejos y a es el coeficiente principal de f(x).


No hay comentarios:
Publicar un comentario