lunes, 27 de mayo de 2013
video de internet desde youtube
este video habla de tres temas que se encuentra en youtube los temas siguientes son:
funciones
division sintetica
logaritmos
http://www.youtube.com/watch?v=Dk5rWtVGyBo
domingo, 28 de abril de 2013
BLOQUE 6 Función racional
BLOQUE
6
Función
racional
donde P y Q son polinomios y x una variable, siendo Q distinto del
polinomio nulo. Las funciones racionales están definidas o tienen sudominio de definición en todos los valores
de x que no anulen el
denominador.1
La palabra "racional" hace
referencia a que la función racional es una razón o cociente (de dos
polinomios); los coeficientes de los polinomios pueden ser números racionales o no.
Las funciones racionales tienen diversas
aplicaciones en el campo del análisis numérico para interpolar o aproximar los
resultados de otras funciones más complejas, ya que son computacionalmente
simples de calcular como los polinomios, pero permiten expresar una mayor
variedad de comportamientos.
Ejemplos
Función homográfica:
si el denominador es distinto de cero, y si
ad ≠ bc, la curva correspondiente es una hipérbola equilátera.2
[editar]Propiedades
·
Todas las funciones racionales en las que el grado de Q sea mayor o igual que el grado de P
tienen asíntotas (verticales, horizontales u oblicuas).
[editar]Integración de funciones racionales
Dada una función racional:
Ejemplos
Asíntotas
horizontales
Las asíntotas horizontales se
refieren a la tendencia de una función. Las tendencias se descubren calculando
los límites de la función para valores muy grandes (infinitos) o para valores
muy negativos (menos infinito).Las asíntotas horizontales pueden ser bilaterales en un mismo valor, bilaterales con diferente valor, o unilaterales.
Hay funciones en las cuales las asíntotas horizontales no se tocan ni cruzan, hay otras en las cuales sí se puede cruzar la asíntota horizontal. En este espacio, veremos los dos casos. No hay que confundir, que las asíntotas verticales no se pueden tocar ni cruzar, ya que ellas dependen de las no definiciones de la función, y si la función no está definida en una asíntota vertical, no puede adoptar el valor de x de la asíntota vertical.
La forma de cálculo de las asíntotas horizontales ya se estudió en el capítulo de límites, en los límites hacia infinito.
Aquí se van a analizar funciones que presentan asíntotas horizontales:
1.- Desde el punto de vista funciones racionales sólo hay dos tipos que presentan asíntotas horizontales; las que tienen el grado del numerador igual o menor que el grado del denominador.
2.- También presentan asíntotas horizontales algunas funciones exponenciales así como algunas logarítmicas.
Asíntotas verticales
Una asíntota vertical es una recta vertical, a la cual se acerca la función sin tocarla nunca.
OJO: No debe confundirse la condición de que una asíntota vertical no se toca o cruza, con el hecho, de que las funciones sí pueden cruzar o tocar una asíntota horizontal.
Para que una función tenga una o varias asíntotas verticales, se tienen que cumplir las siguientes condiciones:
1.- En x = a, la función no está definida, o sea, x = a no es parte del dominio de la función. Por esto no la puede tocar.
2.- El límite cuando x tiende a "a" de la función no existe, pero tiene que haber una tendencia de la función hacia valores extremadamente grandes (infinito) ó extremadamente negativos (menos infinito). Puede darse el caso, de que acercándose por ambos lados al valor de x = a, la tendencia del valor de la función sean ambos infinitos ó ambos menos infinito.
NOTA: Una asíntota vertical puede provocar en la función un cambio de concavidad en la función de antes de la asíntota a después de la asíntota. Analícense algunas de las gráficas de las funciones a continuación. En las primeras dos gráficas hay un cambio de concavidad antes y después de la asíntota vertical.
BLOQUE 5 División sintética
DIVISIÓN SINTETICA
La
división sintética se realiza para simplificar la división de un polinomio
entre otro polinomio de la forma x – c, logrando una manera mas compacta y
sencilla de realizar la división.
Ilustraremos
como el proceso de creación de la división sintética con un ejemplo:
Comenzamos
dividiéndolo normalmente
Teorema fundamental del algebra
El teorema fundamental
del álgebra establece que todo polinomio de una variable no
constante con coeficientes complejos tiene un raíz
compleja, es decir, existe un número complejo que evaluado en el polinomio da
cero. Este incluye polinomios con coeficiente reales, ya que cualquier
número real es un número complejo con parte
imaginaria igual a cero.
Aunque ésta en principio parece ser una
declaración débil, implica todo polinomio de grado n de una variable no
constante con coeficientes complejos n tiene, contando con
lasmultiplicidades, exactamente n raíces. La
equivalencia de estos dos enunciados se realiza mediante la división polinómica sucesiva por factores
lineales.
Hay muchas demostraciones de este importante
resultado, que requieren bastantes conocimientos matemáticos para
formalizarlas. El nombre del teorema es considerado ahora un error por muchos
matemáticos, puesto que es más un teorema del análisis matemático que del álgebra.
Teorema
de factorización lineal
El teorema fundamental del ·lgebra (TFA) dice
que "toda ecuaciÛn polinÛmica
de grado n con coeÖcientes complejos tiene n
raÌces complejas".
De hecho existen m˙ltiples formulaciones
equivalentes; por ejemplo que todo
polinomio real puede expresarse como producto
de factores reales lineales y
cuadr·ticos. 1
Los primeros estudios de las ecuaciones de
Al-Khwarizmi (c 800) sÛlo permitÌan las raÌces reales positivas y, por tanto, el
TFA no tenÌa relevancia alguna.
Fue Cardano el primero en darse cuenta de que
se podÌa trabajar con cantidades
m·s generales que los n˙meros reales. Este
descubrimiento lo hizo estudiando
la ecuaciÛn c˙bica con el Ön de encontrar una
fÛrmula para encontrar sus raÌces.
Cuando aplicÛ su fÛrmula a la ecuaciÛn x
3 = 15x + 4 obtuvo una soluciÛn que
incluÌa p
121, cuando Cardano sabÌa que la soluciÛn
debÌa ser x = 4. A pesar
de que Cardano fue capaz de manipular estos
ín˙meros complejosí, la realidad
es que Èl mismo no los entendiÛ en profundidad
BLOQUE 5 UTILIZAS FUNCIONES FACTORIZABLES EN LA RESOLUCION DE PROBLEMAS
BLOQUE 5
UTILIZAS FUNCIONES FACTORIZABLES EN LA
RESOLUCION DE PROBLEMAS
Llamamos ceros o raíces de una función f a los valores de x para los cuales se cumple que f(x)=0. Los ceros de una función son las abscisas de los puntos en los cuales su gráfica tiene contacto con el eje de las x.
ACTIVIDAD 6:
Indicá los ceros de cada una de las funciones de la Actividad 5.
Recordá: Para hallar los ceros de una función de manera analítica, basta con igualar la ecuación a cero.
Ejemplo:
f(x)=x-2 Cero de f: x=2
x-2=0
x=0+2
x=2
Ejercicio 1:
función polinómica:
f(x) = 2x3 + 7x2 - 7x - 12
Y nos piden hallar los ceros. Los ceros o raíces de una función son las "x" para las cuales la "y" (ó f(x)) vale cero. Es decir: son los números a los cuales, si le aplicas la función, el resultado dá cero. Se pueden hallar "igualando a cero" la fórmula de la función, que es lo mismo que "reemplazar por cero" a la "y" o a f(x) de la fórmula:
2x3 + 7x2 - 7x - 12 = 0
f(x) = 2x3 + 7x2 - 7x - 12
Y nos piden hallar los ceros. Los ceros o raíces de una función son las "x" para las cuales la "y" (ó f(x)) vale cero. Es decir: son los números a los cuales, si le aplicas la función, el resultado dá cero. Se pueden hallar "igualando a cero" la fórmula de la función, que es lo mismo que "reemplazar por cero" a la "y" o a f(x) de la fórmula:
2x3 + 7x2 - 7x - 12 = 0
Ejercicio 2:
f(x) = x2 +
x - 12
|
x2 +
x - 12 = 0
|
Igualando
a cero.
|
(x +
4)(x - 3) = 0
|
Factorizando.
|
x = - 4
|
Solución
1
|
x = 3
|
Solución
2
|
Teoremas
del factor y del residuo
·
Algoritmo
de la división. Para cada polinomio
de grado mayor o igual a uno y para cada número
, existe un polinomio único
de un grado menor que el de
y un número único R, tal que:
Al polinomio
·
Teorema del
residuo. Si
es el residuo de dividir el polinomio
entre
, entonces
.
Demostración.
Como
O sea,
Ejemplo 1:
Hállese el residuo de dividir el polinomio
O sea que el residuo es 2.
·
Teorema del
factor. Si
es un cero del polinomio
, entonces
es un factor de
.
Demostración.
Si
Pero por el algoritmo de la división
Como
Por tanto,
Ejemplo 2:
Use el teorema del factor para probar que
Luego –1 es un cero de
Así
Division
sintetica
La división sintética es un
procedimiento "abreviado" para determinar el cociente y el residuo
que se obtiene al dividir un polinomio
de grado
, por un polinomio de la forma
, con
, a partir de los coeficiente de
y el cero de
.
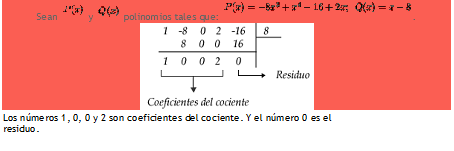
Ejemplo 1 :Sean
Teoremas
del factor y del residuo
El Teorema Fundamental del
Algebra (TFA) dice que todo polinomio a coeficientes complejos tiene un raíz
compleja, es decir existe un número complejo donde el polinomio evalúa a cero.
Hay muchas demostraciones de este importante resultado. Todas requieren
bastantes conocimientos matemáticos para formalizarlas, por ejemplo la división
sintética, el teorema del factor incluso el teorema del residuo. Sin embargo,
si se deja de lado algo del rigor matemático, hay argumentos simples y creíbles,
que le permiten a uno convencerse de la veracidad del TFA.
Este teorema resulta de suma
importancia dentro del estudio de las ecuaciones. Encontrar la solución de una
ecuación representa encontrar todos los valores de x para los cuales la
ecuación es cierta, a las que comúnmente le llamamos raíces de la ecuación,
generalmente las soluciones que de manera inmediata nos interesan son los
valores que existan en los reales, sin que con ello las soluciones complejas no
sean interesantes.
Teorema de factorización lineal
Si f(x) es
un polinomio de grado n, con n > 0, entonces f(x) tiene precisamente n
factores lineales, es decir:
f(x) = a(x – c1)(x – c2)....(x – cn),
factores lineales, es decir:
f(x) = a(x – c1)(x – c2)....(x – cn),
en donde
c1, c2, .....cn son números complejos y a es el coeficiente principal de f(x).
Suscribirse a:
Comentarios (Atom)